Динамическое построение дерева на основе строк списка.
В предыдущих статьях мы рассмотрели построение дерева в статическом и динамическом режимах.
Теперь разберём задачу, которая имеет скорее теоретическое (обучающее), чем прикладное значение. Однако, если у вас хватит терпения пробраться через довольно сложные логические построения, приведённые в статье, вы будете вправе быть собою весьма довольными.
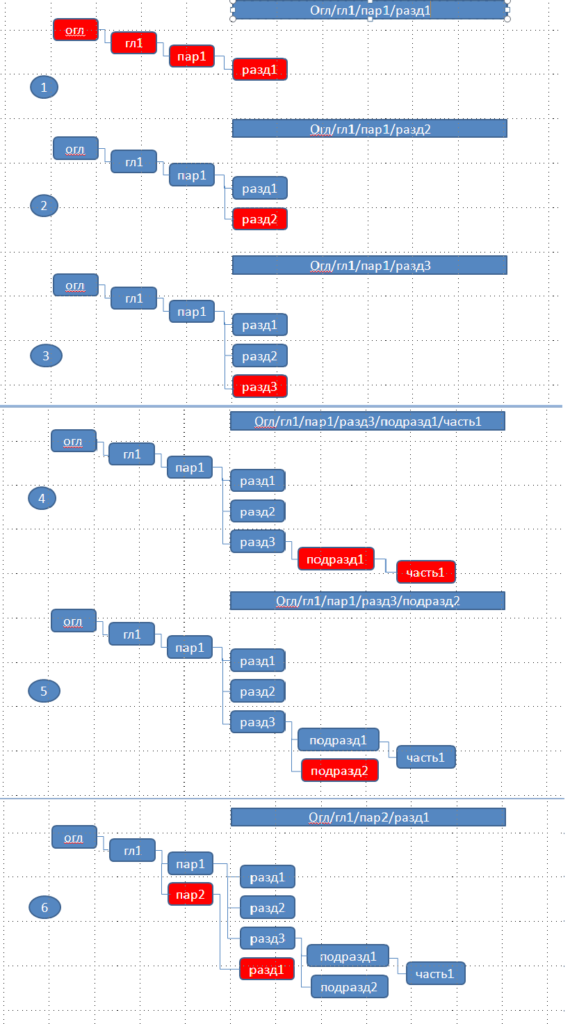
Пусть нам надо создать дерево, отображающее оглавление книги в процессе её создания. Предположим, что на какой-то момент структура книги имеет следующий вид:
То есть оглаление разбито на главы, главы имеют паранрафы, параграфы имеют разделы и так далее.
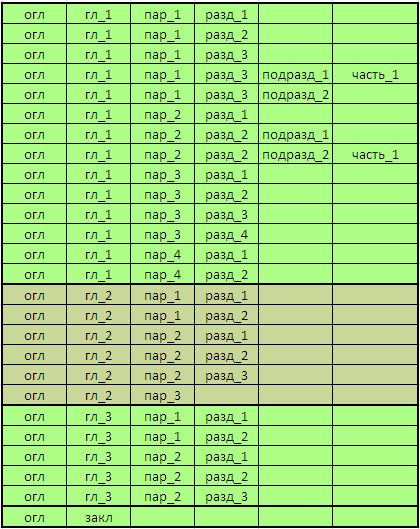
Создадим список, строками которого будут следующие записи:
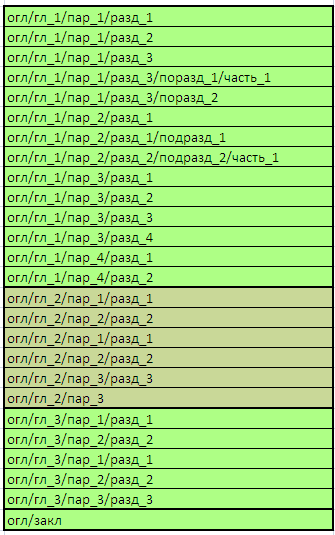
В итоге мы должны получить следующее дерево:

Введём обозначения.
Подстроки между косыми чертами (слешами) назовём «ключами».
Например, в строке«огл/гл1/пар1/разд1» подстроками (ключами) будут «огл, гл1, пар1, разд1».
Приведём пример части существующего дерева.
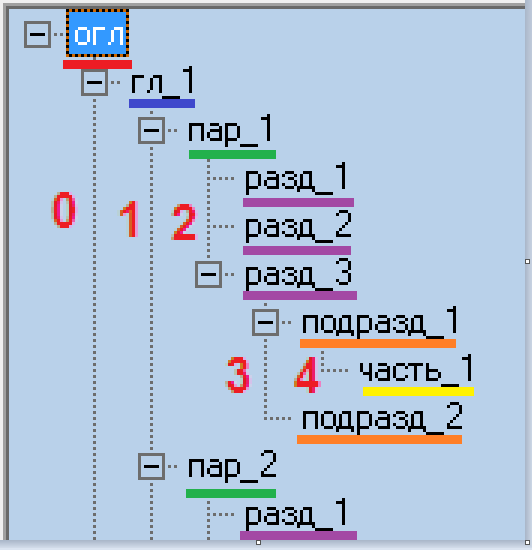
На рисунке цифрами обозначены уровни (штриховые вертикальные линии), на которых расположены соответствующие узлы (каждый уровень выделен своим цветом).
Например, уровень номер три, обозначен фиолетовым цветом.
Узел «огл» является корневым (родительским) узлом для всего дерева.
Последовательности узлов, «произрастающих» из корня, называются «ветвями» дерева. Например, на рисунке приведена одна из ветвей дерева, образованная следующими узлами: «огл, гл1, пар1, разд1, разд2, разд3, подразд1, подразд2, часть1».
Последовательность узлов от корня до какого либо крайнего узла назовём «цепочкой». Например, последовательность узлов: «огл, гл1, пар1, разд1».
И, наконец, термин «гроздь», который мы будем использовать при создании программы, включает узлы одного уровня в данной ветви. Например, узлы «разд1, разд2, разд3».
Принципы построения программы.
Общая укрупнённая блок схема алгоритма вычислений будет иметь вид:
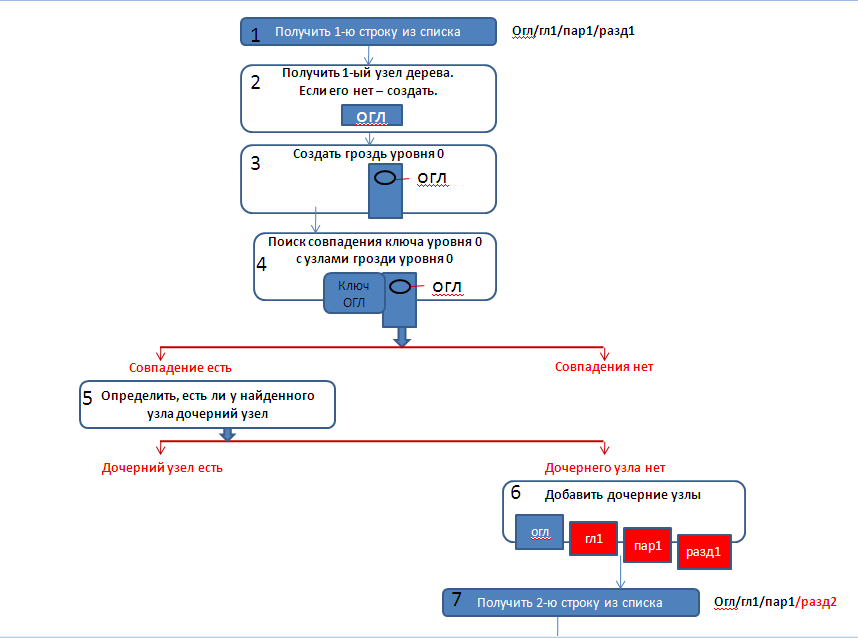

Детальное рассмотрение элементов блок-схемы.
Рассмотрим отдельные элементы блок-схемы подробнее.
1) На первом шаге построим корневой узел и все узлы, соответствующие ключам в первой строке списка:

В результате мы должны получить цепочку узлов, изображённую на рис. 1 под цифрой «1».

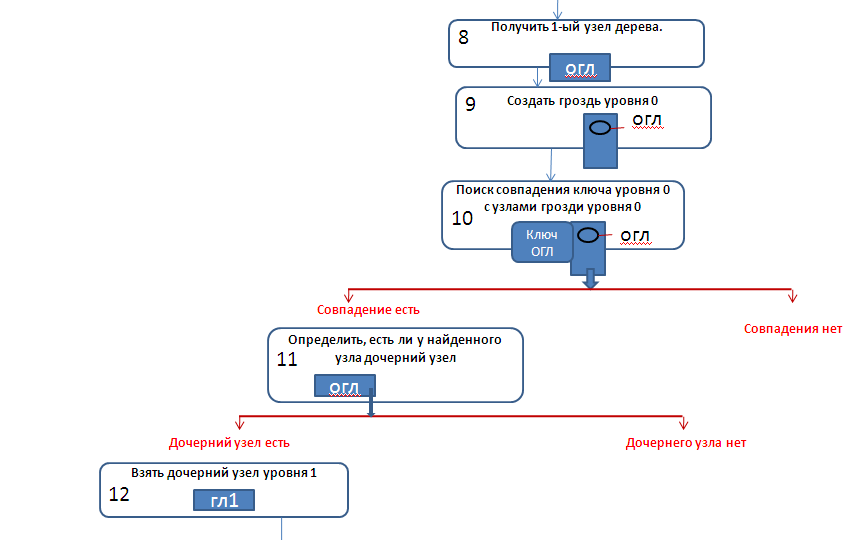
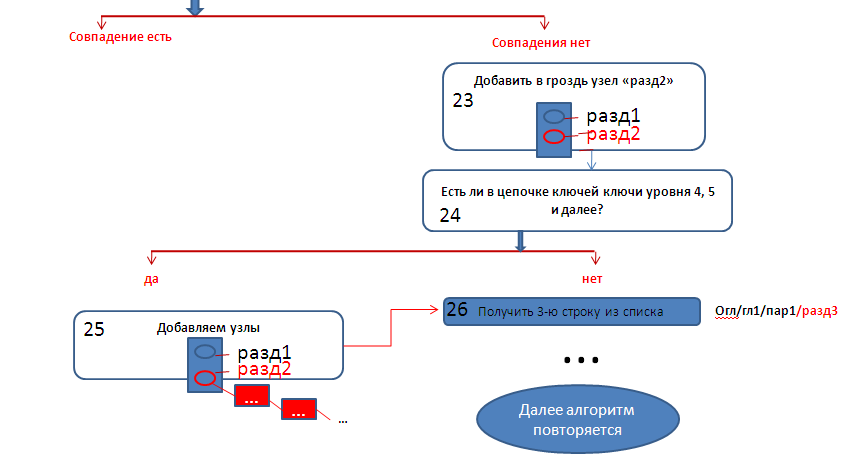
2) Далее построение дерева будет осуществляться по следующему алгоритму:
2.1) Берём вторую строку списка.

2.2) На основание строки строим массив, соответствующий всем узлам нулевого уровня.
2.3) Строим гроздь на нулевом уровне. Так как на нулевом уровне находится только один узел, то гроздь будет содержать только один узел.
А в строке списка нулевому уровню соответствует ключ «огл».
2.4) Организуем поиск, есть ли совпадение ключа с каким либо узлом в грозди. В данном случае это совпадение есть.
2.5) Затем с помощью соответствующей функции ищем первый дочерний узел по отношению к узлу «огл» (то есть перходим на следующий уровень дерева). Это будет узел «гл_1», лежащий на первом уровне.
В строке ключей первому уровню соответствует ключ «гл_1».
2.6) Для первого уровня строим гроздь узлов, опираясь на узел «гл_1» (как это делается конкретно, быдет ясно в дальнейшем).
2.7) Ищем совпадение ключа с одним из узлов грозди (в нашем случае пока в грозди только один узел).
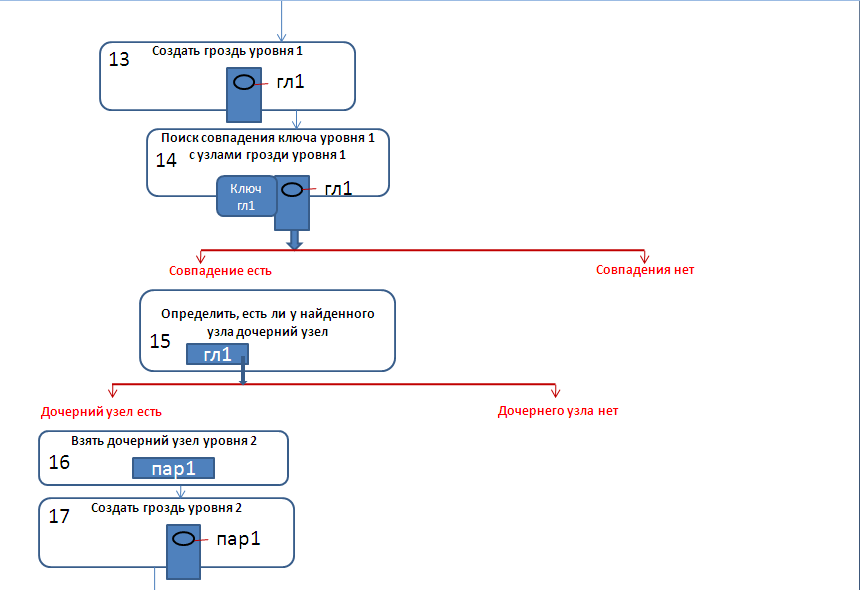
2.7) Аналогичным образом переходим ко второму и третьнму уровням.
Но в грозди третьего уровня нет узлов, совпадающих с ключом «разд_2».
Поэтому добавляем ключ «разд_2» в гроздь третьего уровня.
2.8) В списке ключей нет ключей четвертого и более уровней, поэтому завершаем данный этап строительства дерева.
В результате дерево приобретёт вид:
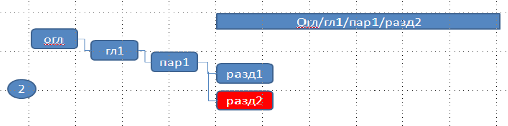
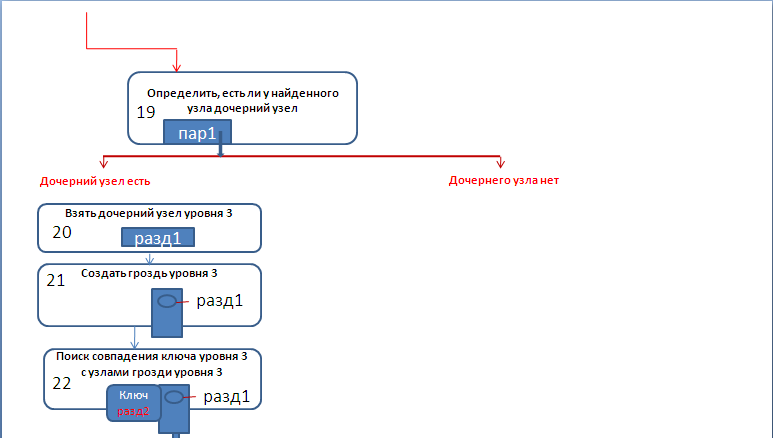
3) Аналогично добавится ещё один узел:
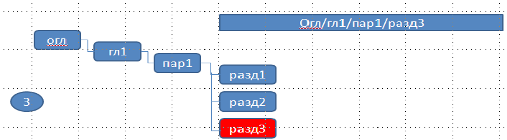
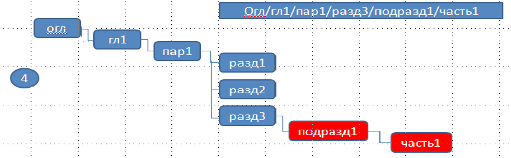
4) Рассмотрим четвёртую строку списка:

На третьем уровне построена гроздь, состоящая из трех узлов «разд_1, разд_2, разд_3». Ключ, соответствующий третьему уровню, равен «разд_3».
Совпадение найдено, но у данного узла нет дочерних узлов. Поэтому цепочка узлов «огл, гл_1, пар_1, разд_3» будет дополнена. Для узла «разд_3» будет построен дочерний узел, соответствующий ключу «подразд_1» и, далее, для узла «подразд_1», строим дочерний узел «часть_1». В результате будем иметь:
5) Следующая строка списка

Программа дойдёт до грозди «подразд_1» и не найдёт совпадения с ключом «подразд_2». Это послужит признаком необходимости добавит ключ в гроздь:
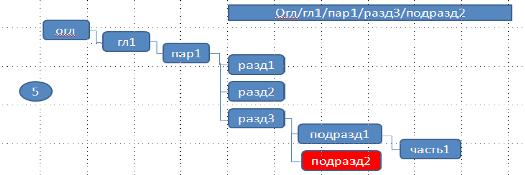
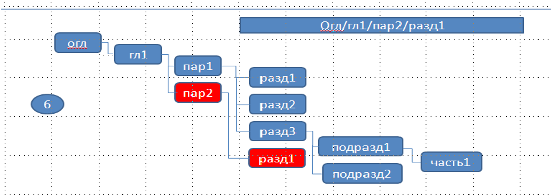
6) И, наконец, строка:

Программа на втором уровне построит гроздь из одного значения «пар_1». Оно не совпадает со значением ключа соответсвующего уровня «пар_2».
Поэтому добавляем в гроздь значение ключа. Так как у нас есть ключ следующего уровня, добавляем его в качестве дочернего по отношению к ключу «пар_2». В результате будем иметь:
Все остальные узлы добавляются в соответствии с рассмотренными вариантами.
Блоки программы
Рассмотренные этапы добавления узлов в дерево позволяют разбить код программы на блоки.
ГЛАВНЫЙ БЛОК.
Цикл выборки строк из списка. Описание блока.

Оформим это описание в блок-схему:
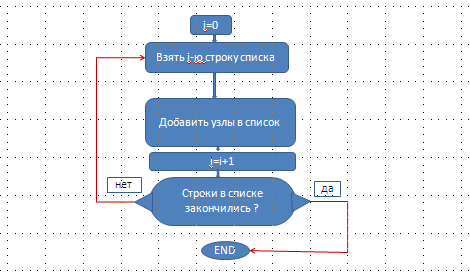
Данной блок-схеме будет соответсвовать следующий код:
procedure TForm1.BitBtn1Click(Sender: Tobject);
var s:string; i:integer;
begin
For i:=0 to self.ListBox1.Count-1 do
begin
s:=self.ListBox1.Items[i];
pr_BLOCK0(s);
end;
end;
БЛОК 0
Добавить в дерево узлы в соответствие с ключами строки.
Задача этого блока — добавить в дерево цепочку узлов. Узлы для добавления определяются на основании анализа ключей, взятых из очередной строки, и уже имеющихся в дереве узлов.
На начальном шаге, когда берётся первая строка из списка, в дереве ещё нет узлов. За построение первого узла будет отвечать БЛОК1.
Все остальные узлы будут добавляться в БЛОК2.

Код, реализующий БЛОК0:
//построить цепочку узлов, соответствующую строке списка
//st — строка списка
procedure Tform1.pr_BLOCK0(st:string);
var node_bunch:TTReeNode;
ARR_of_KEYS:T_ARR_of_KEYS;
rec:T_REC;
begin
//bunch -гроздь;
//rec содержит: массив ключей и первый узел грозди;
//f_BLOCK1 — создать первый узел;
rec:=f_BLOCK1(st);
//ARR_of_KEYS — массив ключей;
ARR_of_KEYS:=rec.ARR_of_KEYS;
//node_bunch — первый узел грозди;
node_bunch:=rec.node;
//pr_BLOCK2 — вставить остальные узлы;
pr_BLOCK2(node_bunch,ARR_of_KEYS);
end; //proc
Реализация BLOCK1
Укрупнённая блок-схема для БЛОК1.

Блок-схема реализуется следующим кодом:
function Tform1.f_BLOCK1(st:string):T_REC;
var node:TTreeNode; rec:T_REC; ARR_of_KEYS:T_ARR_of_KEYS; key:string;
begin
//создать массив ключей
ARR_of_KEYS:=f_GET_ARR_of_KEYS(st);
//получить первый ключ
key:=ARR_of_KEYS[0];
//пытаемся получить самый первый узел дерева
node:=self.TreeView1.Items.GetFirstNode;
//если такого узла нет, то метод возвращает nil;
if node=nil then
//добавляем в дерево первый узел;
node:=self.TreeView1.Items.AddFirst(nil,key);
//формируем возвращаемое значение, заполняя поля записи
rec.node:=node;
rec.ARR_of_KEYS:= ARR_of_KEYS;
//возвращаем значение
result:=rec;
end;
В метд f_GET_ARR_of_KEYS в качестве аргумента передается строка из списка. Например, «огл/гл1/пар1/разд1».
Метод GetFirstNode возвращает ссылку на первый узел в дереве. Усли первого узла нет (дерево пустое), то функция возвращает «nil».
Для создания первого узла используется метод AddFirst(узел,название_узла). Метод добавляет в дерево узел того же уровня, что и уровень узла «узел». Новый узел вставляется после узла «узел». Так как мы хотим, чтобы узел был самым первым, то в качестве предыдущего узла указываем «nil» (нулевая ссылка).
Метод возвращает значение типа запись «ссылка_на_узел, массив_строк».
Функция f_GET_ARR_of_KEYS.
Функция в качестве аргумента принимает строку и возвращает массив строк (ключей). Ключи формируются путём анализа и разбора (парсинга) переданной в функцию строки.
Алгоритм работы функции представлен на следующем рисунке:
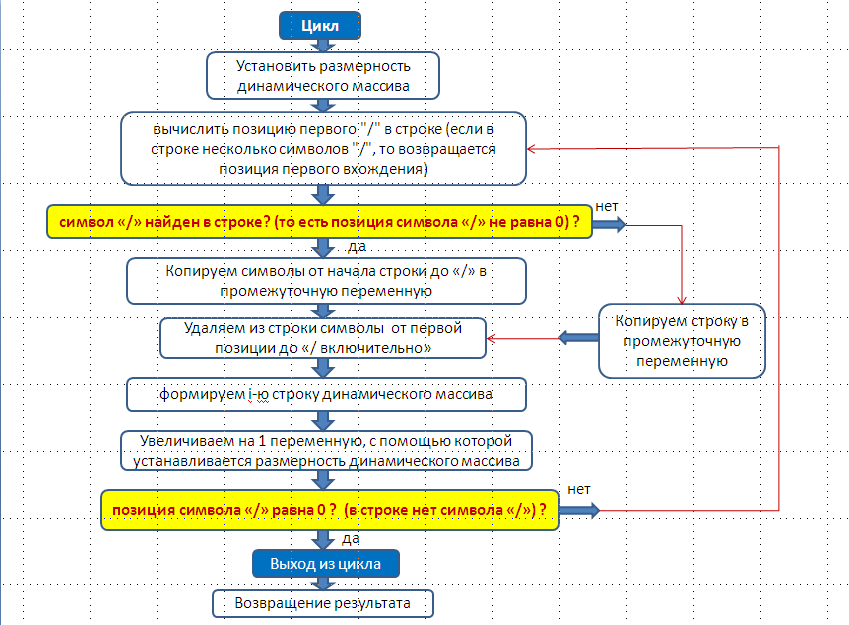
Код функции имеет следующий вид:
//получить массив ключей
function Tform1.f_GET_ARR_of_KEYS(st:string):T_ARR_of_KEYS;
var s,ss:string; i,ps:integer;
arr_key:T_ARR_of_KEYS;
begin
i:=0;
ss:=»;
repeat
setlength(arr_key,i+1);
//определить позицию символа «/»
ps:=pos(‘/’,st);
//копируем от первой позиции до символа «/»
if ps<>0 then
//если ps<>0, то в промежуточную переменную записываем подстроку
ss:=copy(st,1,ps-1);
else
//если ps=0, (в строке нет символа «/»), то записываем остаток строки
ss:=st
//удаляем от первой позиции до символа «/» включительно
delete(st,1,ps);
arr_key[i]:=ss;
inc(i);
until ps=0;
result:=arr_key;
end;
Сначала «обнуляем» локальные переменные (это правило хорошнго тона). Кроме того, это может избавить в дальнейшем от трудно дианосцируемых ошибок.
Далее организуем цикл, в котором переданная в функцию строка разбирается на «ключи» (на подстроки).
Цикл организован оператором с постусловием repeat … until (условие). Выход из цикла осуществляется тогда, когда логическое условие возвращает значение «истина» (или по-другому, цикл совершается до тех пор, пока условие не станет истинным).
В цикле анализируется наличие символа «/» в строке с помощью строковой функции pos(символ, строка) Функция возвращает номер позиции символа в строке.
Первым оператором цикла устанавливается размерность динамического массива с помощью процедуры setlength(массив,размерность).
Далее определяем положение позиции символа «/» в строке «st». Если символ присутствует, («pos<>0»), то копируем часть строки с помощью строковой функции copy(строка,начальная_позиция_копирования,конечная_позиция_копирования) в промежуточную переменную «ss».
Если символ «/» не найден («pos=0»), то копируем все символы в промежуточную переменную «ss».
Далее урезаем строку, удаляя символы из строки с помощью строковой функции delete(строка,начальная_позиция,кончная позиция). Если конечная позиция меньше начальной позиции, то символы не удаляются.
Далее формируем i-ю строку динамическогго массива и увеличиваем счётчик строк i с помощью целочисленной процедуры inc(переменная, число). Эта процедура увеличивает целочисленную переменную на величину, равную второму аргументу «число». Если второй аргумент опущен, то по умолчанию переменная увеличивается на 1.
Далее, если «ps<>0», цикл повторяется.
В итоге функция возвращает массив строковых значений («ключей»).
Результирующая блок-схема.